



Ovšem to, že se zlatý řez vyskytuje v poměrech geometrických obrazců či těles, není jeho jediná aplikace. Asi mnozí se podiví nad tím, že se zlatým řezem se setkáváme snad denně a to úplně nevědomky. Prostor, kam zasahuje zlatý řez daleko přesahuje hranice geometrie. Nalezneme ho snad ve všech oblastech, které nějakým způsobem působí na naše smysly, neboť proporce zlatého řezu působí na naše podvědomí velice příjemným dojmem. (Samozřejmě se ozývají i hlasy, které toto zpochybňují. Zde je uveden úryvek z knihy Maria Livia - Zlatý řez, kde jsou vzneseny takové otazníky.) Architektura, malířství, sochařství dokonce i hudba, ve všech těchto uměleckých oborech se zlatý řez více či méně objevuje. V dnešní době i dobrá fotografie a pěkný design webové stránky je uspořádán podle proporcí zlatého poměru.
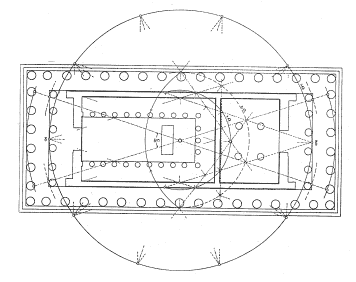
Na antických stavbách si můžeme často všimnout uspořádání nějakého prvku podle zlatého poměru. Jako jeden z největších příkladů bych uvedla chrám Parthenón postavený architektem Iktínem v letech 447 - 432 př. n. l. na athénské Akropoli. Bohužel se nezachovaly žádné plány, takže nemůžeme s jistotou říct, jestli zlaté proporce byly dílem lidského počítání nebo intuice.

antický chrám Parthenón
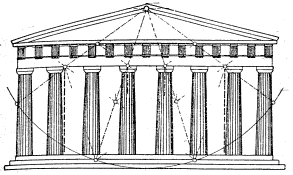
Parthenón - průčelí
Parthenón - půdorys
Ale i v pozdější architektuře nalezneme příklady zlatých poměrů: v gotice se prvky zlatého řezu objevují na chrámu Notre-Dame v Paříži, ve 12. stol. pak v kompozici fasád ruských chrámů, v dílech architekta Le Corbusiera či dokonce v architektuře budovy OSN v New Yorku, ale samozřejmě i mnohde jinde.
Ač je takové uspořádání časté, nelze zlatý řez všeobecně prokázat jako uměleckou přednost před jinými proporcemi.
Co se týče malířů a sochařů i oni používají (většina spíše instinktivně) zlaté proporce ve svých dílech. Zejména v renesanci byl rozšířen názor, že dokonalé proporce lidského těla musí být nutně propojeny se zlatým řezem. Jako pomůcka pro své žáky používali mistři tzv. kánony. Jako nejznámější uvedu Ondřejův kříž, který byl původně kánonem římského stavitele Vitruvia. Podle jeho názoru se výška těla rovná délce rozpjatých končetin a proto lze tedy zakreslit lidské tělo do čtverce. Tomuto čtverci ještě opsal kružnici se středem v pupku, který se tak stává přirozeným středem těla. Tuto "Vitruviovu figuru" převzal i německý malíř Albrecht Dürer a také i všestranný učenec Leonardo da Vinci. Ten se snaží kánon ještě zdokonalit umístěním obdélníků o proporcích zlatého řezu. Jeho dílo "Vitruviova figura" je vskutku známé.
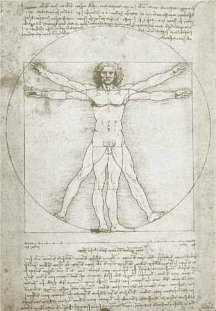
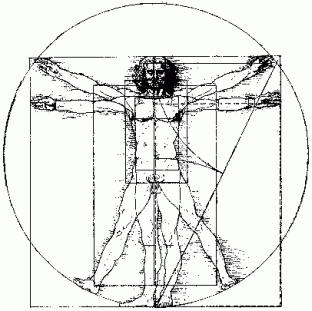

Vitruviova figuraMona Lisa (zlaté proporce)
Co se týče kompozice obrazů, fotografií či webové stránky není vhodné umístit nejdůležitější věci přímo do geometrického středu. Optický střed se totiž nachází v průsečíku dvojitého zlatého řezu, zde je esteticky nejpůsobivější.
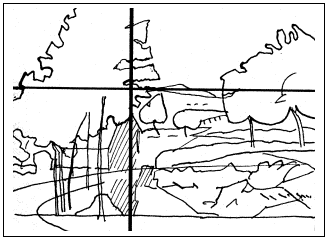
"Zlatý optický střed" (průsečík dvou zlatých poměrů)
Zlatý řez se uplatňuje i v dalším uměleckém směru, tentokrát hudbě. Velice známá je skladba Bély Bartóka Hudba pro smyčce, bicí a celestu. Tato skladba je celá založená na hodnotě zlatého řezu, Bartók zakomponoval zlatý poměr a Fibonacciho čísla opravdu do každé maličkosti od obsazení orchestru po vystupňování celé skladby.

celesta [čelesta] - bicí hudební nástroj, laděný, opatřený pedálem. Rozsah c1 - c5, který se však notuje o oktávu níž. Tento nástroj vynalezl v roce 1886 A. Mustel (1842 - 1919).
V hudebním oboru ještě musím zmínit studii doktora Vladislava Baginského, který podrobil housle typu Stradivari a Guarneri pečlivému zkoumání a došel k překvapivému závěru: oba typy byly pečlivě konstruovány podle zlatých poměrů. Hlavním cílem bylo pravděpodobně dosáhnout optimálního umístění efy.

efa
efy - otvory tvaru písmene f na horní desce houslí, které umožňují přenos zvuku z vnitřku houslí a zajišťují tak mnohem plnější zvuk houslí, mj. také ovlivňují zakřivení víka
Přesuňme se teď z oblasti spíše humanitní na pole působnosti věd přírodních. Samozřejmě i zde se zlatý řez vyskytuje - ve fyzice, v astronomii, ale především v biologii, které se chci v tuto chvíli věnovat trochu podrobněji.
Botaniky dlouhou dobu trápila otázka fylotaxe. Po mnoha odborných studiích došli francouzští badatelé bratři Louis a Antoine Bravais k závěru, že listy rostou na stonku po tzv. genetické spirále, která vystupuje vzhůru podle stáří listů. jednotlivé listy vyrůstají ze středu pod tzv. divergenčním úhlem, jehož hodnota je s malými odchylkami právě 137,5°. Myslím, že v tuto chvíli už snad ani nepřekvapí zjištění, že se jedná o tzv. zlatý úhel.
Úhel, který dělí celou otočku ve zlatém řezu, je totiž 360°/φ = 222,5 stupně. Jelikož je to více než polovina kruhu, měli bychom to měřit v opačném směru. Jinými slovy, měli bychom od 360 odečíst 222,5. Dostaneme tak úhel 137,5 stupně, nazývaný zlatý úhel.
Na podobném principu vyrůstají okvětní lístky růže a dalších rostlin nebo třeba šupiny ananasu. Otázku, proč tomu tak je, zodpověděli fyzikové Douady a Chuder, kteří tvrdili, že při takovém rozmístění listů podléhá rostlina nejmenšímu energetickému zatížení a je pro ni tak nejúspornější. Logaritmické spirály u semen v terči slunečnice, šišek a kaktusů jsem již zmínila v předchozí kapitole.
V této kapitole zmíním logaritmické spirály spojené s živočichy. Jak vzniká logaritmická spirála jsem již uvedla výše a proto jen dodám, že její růst je zajímavý především tím, že zachovává tvar a poměr svých částí - roste stejně do délky i do šířky. Tato asymetrická křivka tedy vyjadřuje symetrický růst, čímž je pro mnohé lidi neskutečně přitažlivá.
Jakub Bernoulli (1654-1705), nejstarší z rodiny vynikajících učenců, se mimo jiné zajímal o zákonitosti křivek. Logaritmická spirála, kterou krátce předtím objevil francouzský filozof a matematik René Descartes, ho přímo fascinovala. Napsal o ní: "...mohla by být symbolem podobnosti potomstva a rodičů, proto chci, aby byla vyryta do mého náhrobního kamene s nápisem Eadem numero mutata resurget" (Volně přeloženo: Ze změn se znovuzrozuje ta samá). Jeho přání se vyplnilo v Bazileji roku 1705.
převzato z diplomové práce Yvety Nagyové - "Užití zlatého řezu" (1995); citace z www.volny.cz/zlaty.rez/diplomka.html (6.6.2007)
Ale zpět ke spirále. Tato křivka vyjadřuje růst neživých částí živého tvora (např. zobáky, zuby, rohy, parohy, schránky apod.). Někdy před sebou vidíme jen část spirály a proto nás hned nenapadne, že třeba ohnutý sloní kel má vlastně mnoho společného s hustě točenou ulitkou plže. Logaritmickou spirálu najdeme u rohů hovězího dobytku a ovcí, u již zmíněného klu slona či dlouhého zubu samce narvala. Jako poslední druh schránkatého hlavonožce žije v mořích Nautilus, jehož schránka je naprosto ukázkovou ilustrací logaritmické spirály. Na průřezu ulitou vidíme přepážky, které rozdělují komůrky, v nichž postupně Nautilus rostl. Když odrostl jedné, postavil si vedle ní další, větší kopii.
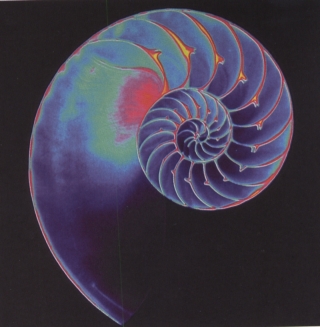
průřez schránkou mořského hlavonožce Nautila
Téměř na závěr ještě malou perličku ze života hmyzu: Hmyz se blíží ke světlu takovým způsobem, aby ho viděl stále pod stejným úhlem. Letí tedy jako kdyby pozpátku po logaritmické spirále.
Jak jsme zjistili, logaritmická spirála je naprosto nezávislá na měřítku a můžeme tedy pozorovat stejnou spirálu u schránky několika milimetrového mořského měkkýše i u mnoho tisíc kilometrů obrovské galaxie. Mezi těmito dvěma krajními body nalezneme spoustu míst, kde se objevují nějaké stopy po zlatém řezu, či jeho aplikacích.