



V planimetrii nalezneme po zlatém řezu mnoho stop. Jako první si z rovinných útvarů uvedeme například tzv. zlatý trojúhelník. Je to takový rovnoramenný trojúhelník, v němž je poměr délky ramene a základny roven Φ. V takovém trojúhelníku jsou úhly při základně rovny 72° a úhel při vrcholu je 36°.
Za další obrazec si zvolíme třeba obdélník, jehož strany a a b budou ve zlatém poměru. Tento zlatý obdélník má následující zajímavou vlastnost. Vepíšeme - li ho do čtverce, budou vrcholy obdélníku dělit strany čtverce právě zlatým řezem. Druhá vlastnost zlatého obdélníku: Oddělíme - li od zlatého obdélníku čtverec s délkou strany rovnou kratší straně obdélníku, bude nově vzniklý obdélník opět zlatým obdélníkem.
Už staří Pythagorovci si vybrali za znak svého bratrstva pěticípou hvězdu, tvořenou úhlopříčkami pravidelného pětiúhelníku. Takový pětiúhelník je bohatým zdrojem zlatých poměrů: Úhlopříčky v pravidelném pětiúhelníku se protínají ve zlatém poměru. Poměr strany a úhlopříčky pravidelného pětiúhelníku je zlatý. Sestrojíme-li všechny úhlopříčky pravidelného pětiúhelníku, dostaneme onu již zmíněnou pěticípou hvězdu, uvnitř které je jiný pravidelný pětiúhelník. (Průsečíky úhlopříček tvoří vrcholy pětiúhelníku). Poměr stran pětiúhelníků je roven Φ2. To jsou jen některé z možností, jak najít v pravidelném pětiúhelníku zlatý řez.
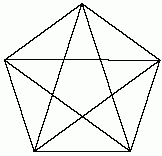
pravidelný pětiúhelník s vyznačenými úhlopříčkami, které tvoří další pravidelný pětiúhelník
V neposlední řadě je i poměr poloměru a strany pravidelného desetiúhelníku zlatý, další rovinné útvary se znaky zlatého řezu nebudu uvádět.
Přeneseme-li se z roviny do prostoru, i zde můžeme najít v tělesech některé vlastnosti spojeně se zlatým řezem. V prostoru můžeme vytvořit právě pět pravidelných mnohostěnů. Jsou to: pravidelný čtyřstěn - tetraedr, pravidelný šestistěn (krychle) - hexaedr, pravidelný osmistěn - oktaedr, pravidelný dvanáctistěn - dodekaedr a pravidelný dvacetistěn - ikosaedr. Tato tělesa byla známa již starověkým Řekům. První, kdo je velmi podrobně popsal byl Platón - jsou po něm proto také pojmenována jako "Platónská tělesa". Platón tato tělesa také považoval ve své teorii za představitele čtyř hlavních živlů: krychle - země, čtyřstěn - vzduch, osmistěn - oheň, dvacetistěn - voda. Dvanáctistěn považoval Platón za představitele jsoucna, neboli všeho, co vůbec existuje.
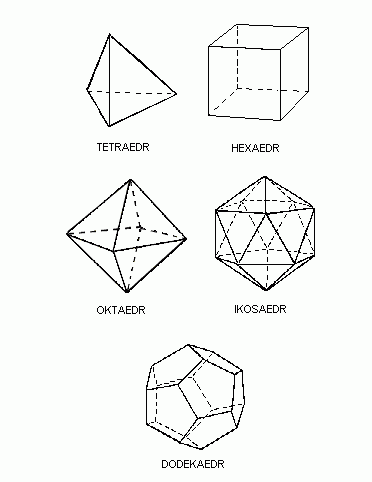
"Platónská tělesa"
O Platóna se později opřel ve své teorii i Johannes Kepler, který tvrdil, že (tehdy 6 známých planet) se pohybuje po kulově ploše opsané nebo vepsané pravidelným mnohostěnům. Tuto teorii ale záhy rozbil fakt, že vzájemná vzdálenost kulových ploch ani zdaleka nemohla odpovídat skutečným vzdálenostem od Slunce.
Ovšem ještě před Keplerem se o Platónská tělesa a jejich souvislost se zlatým řezem zajímal Luca Pacioli ve své knize "O božském poměru". Podrobně prostudoval všech pět těles a našel mnohé vlastnosti související se zlatým řezem. Teorie jsou to vskutku složité a proto je nebudu více rozvádět. Téměř 60 vyobrazení Platónských těles zhotovil pro knihu svého přítele slavný Leonardo da Vinci. Ten se studiem pravidelným mnohostěnů a zlatého řezu zabýval také sám. S oblibou si tělesa zhotovoval z dřevěných konstrukcí, na kterých pak studoval jejich vlastnosti.