



Co se týče uplatnění Fibonacciho posloupnosti v praxi, vyskytuje se především až ve velmi složitých operacích. Z těch nejjednodušších - podle několika pravidel při sčítání, lze najít Fibonacciho čísla v Pascalově trojúhelníku. Dále se využívá tzv. Fibonacciho kódování, které umožňuje kódovat přirozená čísla, převedením na krátké kódové slovo. Každé číslo končí řetězcem "11".
Malou zajímavostí je, že převod mil na kilometry je podle faktoru 1,609 což je téměř hodnota podílu dvou sousedních Fibonacciho čísel. Je-li tedy vzdáleností v mílích jakékoli Fibonacciho číslo, je tato vzdálenost v kilometrech přibližně rovna následujícímu Fibonacciho číslu.
Dalším velmi zajímavým "úkazem" jsou Fibonacciho čtyřúhelníky. Takto se nazývá soubor čtverců, jejichž velikosti stran jsou právě Fibonacciho čísla. Každý nový čtverec má délku strany přesně odpovídající součtu velikostí stran dvou předchozích čtverců. Spirála, zakreslená čtvrtkružnicemi v těchto čtvercích, se nazývá "zlatá spirála". Každá spirála s podobnými vlastnostmi se nazývá logaritmická spirála. Vyskytuje se na mnoha místech v přírodě - tvar ulit mořských měkkýšů, uspořádání semen kvetoucích rostli, či dokonce ve tvaru galaxií a mnohde jinde.
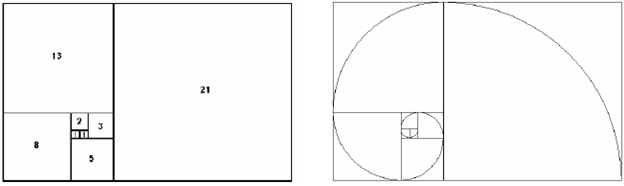
Fibonacciho čtyřúhelníky logaritmická spirála

logaritmická spirála kolem nás - schodiště
V přírodě najdeme stopy po Fibonacciho číslech například i na květinách. Počet okvětních lístků u většiny rostlin je často roven těmto číslům:
1 okvětní lístek: calla lilie, ...
2 okvětní lístky: euforbia, ...
3 okvětní lístky: kosatce, lilie, trilium, ...
5 okvětních lístků: blatouchy, divoké růže, columbine, karafiáty, ...
8 okvětních lístků: celandine, sanguinaria canadensis, stračky, ...
13 okvětních lístků: některé sedmikrásky, třapatky, starčeky, ...
21 okvětních lístků: astry, čekanky, sedmikrásky, ...
34 okvětních lístků: kopretiny, ...
55, 89 okvětních lístků: čeleď hvězdnicovitých, ...
Samozřejmě se takto nedají zařadit všechny rostliny, ale těchto výjimek je opravdu málo.
Uspořádání podle Fibonacciho čísel nalezneme i u semen v terči rostliny, např. slunečnice, která vytváří spirálovité uspořádání. Část semen je ve směru hodinových ručiček a druhá část opačným směrem. Počet spirál není náhodný, ale jedná se vždy o počet odpovídající sousedním Fibonacciho číslům. U slunečnice to bývá většinou 21 a 34 spirál, popř. 34 a 55 spirál. Otázkou zůstává, proč tomu tak je? Nejvíce uznávanou odpověď podali francouzští matematici Y. Couder a S. Douday, kteří tvrdí, že do terče se tím to způsobem vejde největší možné množství semen. Podobné znaky nacházíme ale i u dalších rostlin. Poměrně zřetelně jsou Fibonacciho spirály vidět na šiškách jehličnatých stromů, nejvíce pak na borovici. Šupiny tvoří zase spirály ve směru a proti směru hodinových ručiček, po 8 a po 13 spirálách.
Dalším velmi zajímavým případem v botanice, který je propojen s Fibonacciho posloupností, jsou některé rody kaktusů. U rodů Lophophora, Astrophytum, Stenocactus, Thelocactus a Strombocactus je velmi typický vývoj žeber 5 - 8 - 13 - 21, přičemž nerostou žebra po jednom, nýbrž po více a proto se počet žeber mění "skokem" po číslech Fibonacciho posloupnosti.


Thelocactus hintonii - 21 žeberThelocactus matudae - 13 žeber
Dokonce v samotném lidském těle nalezneme stopy po Fibonacciho posloupnosti. Délka a průměr průdušek vykazují v několika dalších rozvětveních po průdušnici čísla odpovídající Fibonacciho řadě. Vědci nazvali tuto skutečnost Fibonacciho plicním stromem.
Zabrousíme-li do hudby, i zde můžeme nějaká Fibonacciho čísla najít. Například všechny durové stupnice jsou složeny z 8 tónů a 5 půltónů, dohromady tedy 13. Na klavíru je velmi dobře vidět, jak jsou půltóny rozděleny do dvou skupin - po dvou a třech (černé klávesy). Všechna tato čísla samozřejmě patří do Fibonacciho posloupnosti.
Mnoho velkých umělců, mezi nimi i třeba Leonardo da Vinci, používali Fibonacciho posloupnost ke kompozici svým děl. S Fibonacciho posloupností počítají i hráči rulety a je s úspěchem aplikována na kurzové sázky při sportovních utkáních. Na burze má tato posloupnost též dlouhou tradici, především u grafických aplikací, jejichž princip spočívá v tom, že pokud se cena přiblíží liniím vycházejícím z Fibonacciho posloupnosti, lze očekávat změnu trendu. Existuje zde mnoho složitých aplikací.
Toto je výčet pouze některých souvislostí, kde je aplikována Fibonacciho posloupnost. Existuje mnoho míst, na kterých se nevědomky setkáváme s Fibonacciho čísly a některou z jejich vlastností. Některé další uvedu ještě v následující kapitole o "zlatém řezu".