



Co se týče uplatnění Fibonacciho posloupnosti v praxi, vyskytuje se především až ve velmi složitých operacích. Z těch nejjednodušších - podle několika pravidel při sčítání, lze najít Fibonacciho čísla v Pascalově trojúhelníku. Dále se využívá tzv. Fibonacciho kódování, které umožňuje kódovat přirozená čísla, převedením na krátké kódové slovo. Každé číslo končí řetězcem "11".
Malou zajímavostí je, že převod mil na kilometry je podle faktoru 1,609 což je téměř hodnota podílu dvou sousedních Fibonacciho čísel. Je-li tedy vzdáleností v mílích jakékoli Fibonacciho číslo, je tato vzdálenost v kilometrech přibližně rovna následujícímu Fibonacciho číslu.
Dalším velmi zajímavým "úkazem" jsou Fibonacciho čtyřúhelníky. Takto se nazývá soubor čtverců, jejichž velikosti stran jsou právě Fibonacciho čísla. Každý nový čtverec má délku strany přesně odpovídající součtu velikostí stran dvou předchozích čtverců. Spirála, zakreslená čtvrtkružnicemi v těchto čtvercích, se nazývá "zlatá spirála". Každá spirála s podobnými vlastnostmi se nazývá logaritmická spirála. Vyskytuje se na mnoha místech v přírodě - tvar ulit mořských měkkýšů, uspořádání semen kvetoucích rostli, či dokonce ve tvaru galaxií a mnohde jinde.
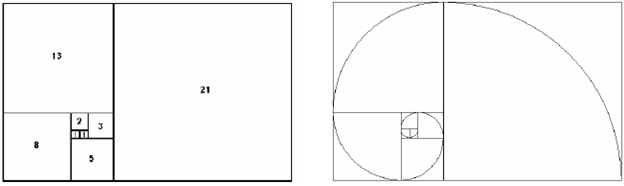
Fibonacciho čtyřúhelníky logaritmická spirála

logaritmická spirála kolem nás - schodiště